Page 51 - Математик

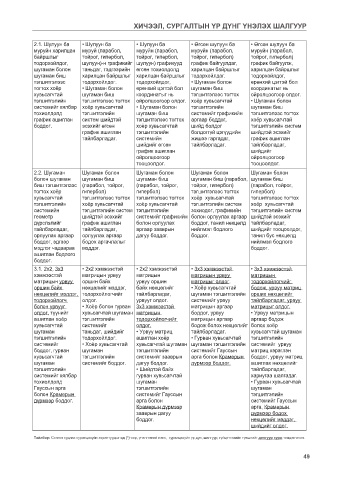
ХИЧЭЭЛ, СУРГАЛТЫН ҮР ДҮНГ ҮНЭЛЭХ ШАЛГУУР

2.1. Шулуун ба • Шулуун ба • Шулуун ба • Өгсөн шулуун ба • Өгсөн шулуун ба
муруйн харилцан муруй (парабол, муруйн (парабол, муруйн (парабол, муруйн (парабол,
байршлыг тойрог, гипербол, тойрог, гипербол, тойрог, гипербол) тойрог, гипербол)
тодорхойлдог, шулуун)-н графикийг шулуун) графикууд график байгуулдаг, график байгуулж,
шугаман болон таньдаг, тэдгээрийн өгсөн тохиолдолд харилцан байршлыг харилцан байршлыг
шугаман биш харилцан байршлыг харилцан байршлыг тодорхойлдог. тодорхойлдог,
тэгшитгэлээс тодорхойлдог. тодорхойлдог, • Шугаман болон ерөнхий цэгтэй бол
тогтох хоёр • Шугаман болон ерөнхий цэгтэй бол шугаман биш координатыг нь
хувьсагчтай шугаман биш координатыг нь тэгшитгэлээс тогтох ойролцоогоор олдог.
тэгшитгэлийн тэгшитгэлээс тогтох ойролцоогоор олдог. хоёр хувьсагчтай • Шугаман болон
системийг хялбар хоёр хувьсагчтай • Шугаман болон тэгшитгэлийн шугаман биш
тохиолдолд тэгшитгэлийн шугаман биш системийг графикийн тэгшитгэлээс тогтох
график ашиглан систем шийдтэй тэгшитгэлээс тогтох аргаар боддог, хоёр хувьсагчтай
боддог. эсэхийг өгсөн хоёр хувьсагчтай шийд болдог тэгшитгэлийн систем
график ашиглан тэгшитгэлийн болдоггүй цэгүүдийн шийдтэй эсэхийг
тайлбарладаг. системийн жишээ гаргадаг, график ашиглан
шийдийг өгсөн тайлбарладаг. тайлбарладаг,
график ашиглан шийдийг
ойролцоогоор ойролцоогоор
тооцоолдог. тооцоолдог.
2.2. Шугаман Шугаман болон Шугаман болон Шугаман болон Шугаман болон
болон шугаман шугаман биш шугаман биш шугаман биш (парабол, шугаман биш
биш тэгшитгэлээс (парабол, тойрог, (парабол, тойрог, тойрог, гипербол) (парабол, тойрог,
тогтох хоёр гипербол) гипербол) тэгшитгэлээс тогтох гипербол)
хувьсагчтай тэгшитгэлээс тогтох тэгшитгэлээс тогтох хоёр хувьсагчтай тэгшитгэлээс тогтох
тэгшитгэлийн хоёр хувьсагчтай хоёр хувьсагчтай тэгшитгэлийн систем хоёр хувьсагчтай
системийн тэгшитгэлийн систем тэгшитгэлийн зохиодог, графикийн тэгшитгэлийн систем
геометр шийдтэй эсэхийг системийг графикийн болон орлуулах аргаар шийдтэй эсэхийг
дүрслэлийг график ашиглан болон орлуулах боддог, танил нөхцөлд тайлбарладаг,
тайлбарладаг, тайлбарладаг, аргаар зааврын нийлмэл бодлого шийдийг тооцоолдог,
орлуулах аргаар орлуулах аргаар дагуу боддог. боддог. танил бус нөхцөлд
боддог, эдгээр бодох аргачлалыг нийлмэл бодлого
мэдлэг чадвараа мэддэг. боддог.
ашиглан бодлого
боддог.
3.1. 2x2, 3x3 • 2x2 хэмжээстэй • 2x2 хэмжээстэй • 3x3 хэмжээстэй • 3x3 хэмжээстэй
хэмжээстэй матрицын урвуу матрицын матрицын урвуу матрицын
матрицын урвуу оршин байх урвуу оршин матрицыг олдог. тодорхойлогчийг
оршин байх нөхцөлийг мэддэг, байх нөхцөлийг • Хоёр хувьсагчтай бодож, урвуу матриц
нөхцөлийг мэддэг, тодорхойлогчийг тайлбарладаг, шугаман тэгшитгэлийн орших нөхцөлийг
тодорхойлогч олдог. урвууг олдог. системийг урвуу тайлбарладаг, урвуу
болон урвууг • Хоёр болон гурван 3x3 хэмжээстэй матрицын аргаар матрицыг олдог.
олдог, түүнийг хувьсагчтай шугаман матрицын боддог, урвуу • Урвуу матрицын
ашиглан хоёр тэгшитгэлийн тодорхойлогчийг матрицын аргаар аргаар бодож
хувьсагчтай системийг олдог. бодож болох нөхцөлийг болох хоёр
шугаман таньдаг, шийдийг • Урвуу матриц тайлбарладаг. хувьсагчтай шугаман
тэгшитгэлийн тодорхойлдог. ашиглан хоёр • Гурван хувьсагчтай тэгшитгэлийн
системийг • Хоёр хувьсагчтай хувьсагчтай шугаман шугаман тэгшитгэлийн системийг урвуу
боддог, гурван шугаман тэгшитгэлийн системийг Гауссын матриц хэрэглэн
хувьсагчтай тэгшитгэлийн системийг зааврын арга болон Крамерын боддог, урвуу матриц
шугаман системийг боддог. дагуу боддог. дүрмээр боддог. ашиглах нөхцөлийг
тэгшитгэлийн • Шийдтэй байх тайлбарладаг,
системийг хялбар гурван хувьсагчтай хариугаа шалгадаг.
тохиолдолд шугаман • Гурван хувьсагчтай
Гауссын арга тэгшитгэлийн шугаман
болон Крамерын системийг Гауссын тэгшитгэлийн
дүрмээр боддог. арга болон системийг Гауссын
Крамерын дүрмээр арга, Крамерын
зааврын дагуу дүрмээр бодох
боддог. нөхцөлийг мэддэг,
шийдийг олдог.

Тайлбар: Сонгон судлах суралцахуйн зорилтуудыг од (*)-оор, үнэлгээний нэгж, суралцахуйн үр дүн, шалгуур, гүйцэтгэлийн түвшнийг доогуур зурж тэмдэглэсэн.

49