Page 33 - Физик
P. 33
СУРАЛЦАХУЙН ҮР ДҮНГИЙН ШАЛГУУРЫГ ХЭРЭГЛЭХ ЗӨВЛӨМЖ
Асуултын хувилбар №4. Араат дамжуургын хувьд хүрднүүдийн хувьд ижил ба ялгаатай зүйлийг
харьцуулахыг хүснэ (задлан шинжлэх).
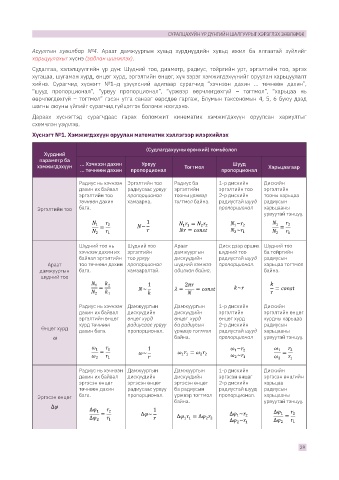
Судалгаа, хэлэлцүүлгийн үр дүн: Шүдний тоо, диаметр, радиус, тойргийн урт, эргэлтийн тоо, эргэх
хугацаа, шугаман хурд, өнцөг хурд, эргэлтийн өнцөг, хүч зэрэг хэмжигдэхүүнийг оруулан харьцуулалт
хийнэ. Сурагчид хүснэгт №1–д үзүүлсний адилаар сурагчид “хэчнээн дахин ... төчнөөн дахин”,
“шууд пропорционал”, “урвуу пропорционал”, “үржвэр өөрчлөгдөхгүй – тогтмол”, “харьцаа нь
өөрчлөгдөхгүй – тогтмол” гэсэн утга санааг өөрсдөө гаргаж, Блумын таксономын 4, 5, 6 буюу дээд
шатны оюуны үйлийг сурагчид гүйцэтгэх боломж нээгдэнэ.
Дараах хүснэгтэд сурагчдаас гарах боломжит кинематик хэмжигдэхүүн оруулсан хариултыг
схемчлэн үзүүлэв.
Хүснэгт №1. Хэмжигдэхүүн оруулан математик хэллэгээр илэрхийлэх
(Судлагдахууны ерөнхий) томьёолол
Хүрдний
параметр ба
хэмжигдэхүүн ... Хэчнээн дахин Урвуу Тогтмол Шууд Харьцаагаар
... төчнөөн дахин пропорционал пропорционал
Радиус нь хэчнээн Эргэлтийн тоо Радиус ба 1-р дискийн Дискийн
дахин их байвал радиусаас урвуу эргэлтийн эргэлтийн тоо эргэлтийн
эргэлтийн тоо пропорционал тооны үржвэр 2-р дискийн тооны харьцаа
төчнөөн дахин хамаарна. тогтмол байна. радиустай шууд радиусын
Эргэлтийн тоо бага. пропорционал харьцааны
урвуутай тэнцүү.
= ~
1
1 2 1 2 = 1 1 2 2 ~
2
2 2
= = 1 1 1 = 1 2 ~
1 1 2 ~
= ~
=
1
2 1 1 = = 2 2 1 1 = ~ ~ = = 2 2 2 1 1 2 1 2 ~ 2 1 ~ 2 1 = 2
2
2 1
12
1 1 2 2
2
1 1
1
= ~
=
1
2 1 2 ~ 1 ~ = 2 ~ ~ 2 = 1 1 = 2 1 1 2
1
1
12
~
=
2 1
2
2
1
21
1
= ~ 2 1 2 = 1
21
Араат = ~
2
1 2 1 = Шүдний тоо нь Шүдний тоо 1 1 2 2 1 1 = 2 1 2 ~
~
1 1
2 2
1
=
~
2 2 1
1
2
2
2
1 2
1
1 1
= = 1 = 2 2 Диск дээр орших Шүдний тоо 1 2
=
=
дамжуургын 1 ~
хэчнээн дахин их ~
ба тойргийн
~
1
2
1
1
1 2 2 1 2 1 2 1 эргэлтийн = = шүдний тоо ~ 1 2 =
1
=
2 1
2 = 1 2 2 1 = ~ ~ 1 2 2 2 2 ~ 1 1 1 2 = 1 1 = 2 2
~
= 1
~
=
1 2 1
дискүүдийн
1 байвал эргэлтийн тоо урвуу = 2 = радиустай шууд 2 радиусын 1 2 = 1 2
1
1
2 1
1
~ = ~
1
2 2
2
= ~
2
=
=
1 1 2
= =
2
=
2
2
1
1
шүдний хэмжээ ~
пропорционал.
2
2
1
Араат 2 = 2 1 1 2 ~ 1 = = = ~ харьцаа тогтмол = 1 2 1
2
тоо төчнөөн дахин пропорционал 1
=
= =
=
~
~ =
1
байна.
дамжуургын бага. хамааралтай. адилхан байна. ~ ~ ~
шүдний тоо = 2 1
1
2
1
2
= 1 = = 2 1 2 2
2
2 1
2 1 2 1 2 1 1 = ~ ~ 1 1 2 = = = ~ = =
~ =
=
=
=
~
1
~
1
2 2 1 ~ ~ = = 2 ~ = =
=
=
~
Радиус нь хэчнээн Дамжуургын Дамжуургын 1-р дискийн Дискийн
дахин их байвал дискүүдийн дискүүдийн эргэлтийн эргэлтийн өнцөг
эргэлтийн өнцөг өнцөг хурд өнцөг хурд өнцөг хурд хурдны харьцаа
хурд төчнөөн радиусаас урвуу ба радиусын 2-р дискийн радиусын
Өнцөг хурд
дахин бага. пропорционал. үржвэр тогтмол радиустай шууд харьцааны
1 1 байна. пропорционал урвуутай тэнцүү.
2
~
= = = ~ 2
1
2
1
1
1
2
1
1
~
=
1
2 1 1= 2 1 2 2 ~ 1 1 1 2 2 = 1 2 ~ 1 = 1
1 1
2
1
~
1 2
~
2 = 1 = ~ = 2 2 2 2 ~ 2 2 1 = 2
2
1
1 1
1
=
~
~
=
~ ~
=
1 2
2 2 1 1 1 = 2 2 1 ~ 1 1 1 2 2 2 2 1 2 1= 2 1 2
1 1
2 2 2
1 2
~
~ 1
1 1
2 2
2
=
= 1
1 1
2
~
2
2
2
2 1
~ 1 1 2 2 1 1 1
Дамжуургын
Дискийн
1-р дискийн
∆ ~
∆ = ∆
Радиус нь хэчнээн Дамжуургын 2 2 ∆ = ∆ ∆ ~ ∆ 1 ∆
1
∆ ~
дискүүдийн
1 1 1
эргэсэн өнцгийн
дахин их байвал
эргэсэн өнцөг =
2
1
2
1
1
2
=
∆ ~
2
дискүүдийн 2 2
1
∆ ∆ ∆ ~ ∆ ~ 1 ∆ 1 1 1 1∆ 1 ∆ ~ ∆ 1 ∆ =
1
2
2
2 2
∆ ~
∆ = ∆
∆ ~
эргэсэн өнцөг
1 2
эргэсэн өнцөг
=
∆
∆ ∆ 1 = 2 ∆ 1 ∆ 1 2 эргэсэн өнцөг ∆ = ∆ 2 2 2 1 2-р дискийн 1 2 2 2 1 харьцаа ∆ 1= 2 1 2 2
1
1 1
∆
1
∆ ~ ~
∆
1
∆ ~
∆
∆ = ∆
∆ ~
2
∆ ~
∆
∆
1 2
1 2
1 1
2 2
2 2
1 1
∆ =
1
2
1
∆ ~
∆ ~
2
∆
2
=
∆
∆ ~
∆ 2 1 төчнөөн дахин радиусаас урвуу ба радиусын радиустай шууд радиусын 2 = 1 = 1
∆
2
1
∆
∆
∆
1=
∆ ~
∆
2 1
∆ 2 ∆ 1 2 = 2 2 2 1 1 ∆ 2 1 1
2
пропорционал.
= 1
Эргэсэн өнцөг бага. 2 2 1 1 1 үржвэр тогтмол пропорционал. харьцааны
∆
∆
2
∆ 1 2 ∆ ~ ∆ = ∆ ∆ ~ байна. ∆ 1 = 2 урвуутай тэнцүү.
1
2 2
1 1
2
1
∆ ∆ 2 = 1 ∆ ∆ 1 1 2 2 ∆ ~ ∆ = ∆ ∆ ∆ ~ 1 1 2 2 ∆ ∆ 1 1 2 2
∆ ~
∆
∆
1 1
∆ ~
∆ = = ∆
1 1
∆
∆ ~
1 1 ∆
1
∆ ~
1
2
2 2 2 2
1
2
1
∆ ~
∆ 1=
∆ = ∆
∆ 1=
∆ ~
∆
2 2
1 1
1 2
1
∆
1
∆ ∆ 1 ∆ 1 2 = = 2 1 1 ∆ ~ 1 ∆ = ∆ ∆ ~ 2 1 1 ∆ 1 2 = = 2 1 1
2 2
∆ =
∆ =
1 1
∆ ~
∆ ~
∆ ~
∆
∆ ~
2
∆
2
∆ ~ 2
2 2 1
1 1
2 2
2 2 =
2 2 =
∆ ∆ 2 ∆ 1 1 2 ∆ ~ ∆ ∆ 1 1
2 1
1
2 1
2
2 1
∆
∆
1
2
2
2
= 1 = = =
~ ∆ ~ = ~ 1 1 = = =
=
=
= ∆ ~ ∆ ~ 1 1 = = = =
29
=
=
=
=
=
1
∆ ~
∆ ~
=
=
~
=
~
~
~
~
~
~
~ ∆ ~ ~ ~ =
1 2 1 = ~ 1 2
= ~ 1 1 2 2 1 2 =
2 1 1 1 2 2 ~ = = 1 ~ 1 1 2 2
1 1
1
1 1
1 ~
1 1
~
2
1
=
1
~
2
1 2
1 2
2 ~
= = 2
1 = 2 ~ 1 = 2 2 2 2 ~ ~ 2 2 2 1 = 2
~
= = 2
1 1 2 2
1 1
=
1
1 2
=
=
2 2
1
1
1
1 1
1 1
~
~
2 1
2 2 =
2 2
1 1
2 2 =
~ 2
1 1
~
2 1
2 1
2 1 1 ~ 2 ~ 1 2 1 1
2 1
1
2
2
2