Page 127 - Физик
P. 127
СУРАЛЦАХУЙН ҮР ДҮНГИЙН ШАЛГУУР
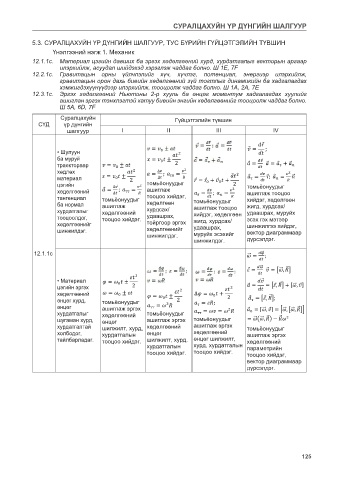
5.3. СУРАЛЦАХУЙН ҮР ДҮНГИЙН ШАЛГУУР, ТУС БҮРИЙН ГҮЙЦЭТГЭЛИЙН ТҮВШИН
Үнэлгээний нэгж 1. Механик
12.1.1с. Материал цэгийн давших ба эргэх хөдөлгөөний хурд, хурдатгалыг векторын аргаар
илэрхийлж, асуудал шийдэхэд хэрэглэж чаддаг болно. Ш 1E, 7F
12.2.1с. Гравитацын орны үйлчлэлийг хүч, хүчлэг, потенциал, энергиэр илэрхийлж,
гравитацын орон дахь биеийн хөдөлгөөний зүй тогтлыг динамикийн ба хадгалагдах
хэмжигдэхүүнүүдээр илэрхийлж, тооцоолж чаддаг болно. Ш 1A, 2A, 7E
= ± 2 ∆ ∆
= ±
⃗
; =
12.3.1с. Эргэх хөдөлгөөний Ньютоны 2-р хууль ба өнцөг моментум хадгалагдах хуулийг ∆ ; = ∆ ; =
=
2
⃗
0
0
⃗ = ⃗ + +
⃗
= ∆
0
⃗ = ⃗ + +
⃗ 0
ашиглан эргэх тэнхлэгтэй хатуу биеийн энгийн хөдөлгөөнийг тооцоолж чаддаг болно. ∆ ; = ∆ ∆
2
0
0
Ш 5A, 6D, 7F 2 2 = ± 2 2 2 = ∆ ∆ ; =
∆
⃗
= ±
2 ∆ ; =
= ± = ± ⃗ = ⃗ 0 2 ⃗ + ⃗ + 2 = ∆ ; = ∆ ; =
0
⃗
; =
∆
∆
⃗
0
2 = ∆
0
⃗ =
0
2 + ⃗ +
0
; = ∆
0
⃗
Суралцахуйн = ± 2 2 Гүйцэтгэлийн түвшин ; = = 0 ⃗ + ⃗ + 2 2 = ± 2 ∆ 2 ∆
0
0
= ±
=
0
2
0
2
0
2
=
; =
2
2 ±
СҮД үр дүнгийн ∆ ⃗⃗ = ± 2 = 2 2 2 = ± 2 2
0
=
± 2
2 0
; =
=
0
⃗
шалгуур I = ∆ ⃗⃗ ; = 0 2 2 III ⃗ = ; = тт = 2 2 = ± 2
= = ± 2
0
⃗
II ; тт
= ∆
⃗
=
;
0
тт
⃗
IV =
∆ 2 = ; ; = тт 2
⃗
∆ ⃗⃗ =
2
= ∆ ⃗⃗ ; = 2 2 2
; =
⃗
∆ ⃗⃗
; = =
; =
=
⃗
= ± ⃗ = ∆ ; тт = ⃗ = ; = тт = 2
; тт
0
;
⃗
= ± ⃗ = ∆ ∆ тт = ⃗⃗ = ⃗; = тт тт
0
⃗ ;
=
⃗
⃗ ⃗ =
2 ⃗
2 = ±
⃗
⃗
• Шулуун = ± = ± = ⃗⃗ = + ∆ = ; =
⃗
2
⃗
= +
⃗
; =
; =
=
; = ; =
0
∆ 2
⃗
∆
ба муруй = ± = 0 0 ± = ± 2 2 = ⃗⃗ ∆ ; = ∆ ∆ = ∆ 0 ; = = ; =
=
⃗
=
2 ; =
0
= ±
⃗ = ⃗ + ⃗ + ⃗⃗ ⃗ = ⃗ + ⃗
0
0
∆ ; = +
= ±
2
∆
⃗ = ⃗ + +
∆ =
= ∆ 2
∆ ⃗ = ⃗ + ⃗
0 ⃗ = ∆
0
∆
; = ∆
2 ⃗ ⃗
траектораар = ± 2 0 ⃗ = ⃗ + ⃗ ⃗ 2 ⃗ 2 0 ⃗; = = 2 ⃗ = ⃗ ; ; = + 2 2 2 2
⃗ 2
⃗
⃗
0
2
0
0
⃗ ⃗ =
∆ + ⃗ =
⃗ = ; =
⃗
0
⃗
⃗ = ⃗ + + 2 ⃗ =
2
0
2
0 2 +
⃗
∆
∆
⃗
= ± ±
хөдлөх = 2 0 = ∆ 0 ∆ ; = 0 2 0 2 2 ⃗; = ∆ ; = 2; = ∆ ∆ = 2 = 2
2 ±0
= 0
2 ⃗ =
2
= +
∆
∆
= ± = ±
= ;
⃗ 2
2
± 2
⃗
= =
0
2
= ± 2 ±
; = = ∆ = +
0 ± = 2
=
= =
0 0 ±
= ± тт ∆ = + 2
2
2
2
0
0
∆ 2
⃗⃗ =
∆
∆ ∆
=
∆ ± 2 ∆
2
материал 0 = ± = 2 0 = ∆ ∆ ; тт тт 2 = ⃗ 2 ; = ⃗ 2 = ⃗ ; = 0 = ∆ ∆ ⃗⃗ ∆ ; 0 ; тт 0 0 2 2 2
= ⃗; ⃗ =
⃗
⃗ = ⃗ 2
⃗
=
⃗ = ⃗ + + + ⃗ +
; =
∆
0 ; = ⃗
; =
= ± =
2
⃗
2
2 = ; =
; =
⃗; ⃗ = ;
0 =
; = =
0 0
⃗
2
= ⃗ = ⃗ +
2 + 2
=
2 2
⃗
∆ ⃗ 0 +
2 ⃗ = ⃗ + ⃗ + = ⃗
0
∆
0
= ±
⃗ ∆
∆
цэгийн 2 2 2 томьёонуудыг 0 + = 2 2 = ± = ∆ 0 0 ⃗; ⃗ ∆ 2 ⃗ 2 ⃗⃗⃗ = = = 2
= ± 2 ∆ =
2
0
2
0
0 2
2 ; =
2 томьёонуудыг
0 2
= =
⃗⃗⃗⃗ ;
∆ 2
∆
∆ ⃗⃗
= ±
2
2
;
2 ⃗ = ⃗
⃗
тт
= [ ⃗, ⃗⃗ ] =
2 ; ⃗ = = ;
= ± хөдөлгөөний = ∆ ⃗⃗ 0 ∆ ⃗⃗; = 0 ⃗ ⃗ ; = ∆ ∆ тт = ∆ 2 = 2 2 2 ⃗ = = = = [ ⃗, ⃗⃗ ] =
⃗
⃗ =
⃗
0
⃗⃗⃗
2
⃗⃗⃗⃗
;
2
2
=
∆ ;
2
⃗⃗⃗
⃗
2
= ± = ± 2
=
= ⃗ =
⃗ =
; ⃗ = ; тт
⃗ 2
; тт
⃗
⃗
⃗
тт
=
0 2 2 2
= ± = ± =∆ = тт 0 ⃗ ; = ⃗ ∆ ; = ∆ 2 ; = ; ашиглаж тооцоо тт= тт
= ± = ±
ашиглаж = ∆
=
=
тт
;
2
2
2 ± 2
тт
0
тт
;
;
= =
⃗ ∆ ⃗⃗ = 0 ±
2
; = ; =
0
=
2
=
⃗
⃗ =
⃗ = ⃗ + +
=
тт ±
⃗
2 ± 2
⃗
2
0
тангенциал 0 = ∆ ∆ ; тт ⃗ 0 = 2 тооцоо хийдэг, = = ∆ = ± = 0 0 2 ⃗ = ⃗⃗⃗ ⃗⃗⃗⃗ ⃗ = [ ⃗⃗⃗, ⃗⃗ ]
∆ 2
= = ∆
⃗ ; = ∆
⃗⃗⃗⃗
± = ± ±
⃗
2
; = =
0
0
хийдэг, хөдөлгөөн
томьёонуудыг
⃗
2
⃗ ⃗∆ ; =
=
⃗ = ⃗ + + 2
0
; =
= ± = ± 2
; = ⃗ = [ ⃗⃗⃗, ⃗⃗ ]
тт
0
⃗⃗⃗ ; ⃗ =
томьёонуудыг
⃗
;
⃗
2 2
⃗;
2
0
0
⃗⃗⃗
2
⃗⃗⃗⃗
2
⃗
⃗
⃗
; =
2
⃗
=
хөдөлгөөн ⃗ = =
⃗
ба нормал = ± ∆ ⃗⃗ 2 = ± ⃗ ; 0 0 = 0 2 ; = 2 = ⃗ ; = = ; ⃗ = = [ ⃗, ⃗⃗ ]
∆ ⃗⃗
⃗⃗ 2
= =
⃗
⃗
⃗
⃗
⃗
= ±
0
2
2
=
;
=
;
= 0 ⃗ =
⃗
; ⃗ =
⃗ =
⃗
⃗
= [ ⃗, ⃗⃗ ]
=
=
⃗
тт =
⃗ ⃗ =
= ± ∆ ⃗⃗ ашиглаж тт ∆ ⃗⃗; 2 ⃗ = = ⃗⃗ = + ⃗ ; ⃗2 ⃗⃗ жигд, хурдсах/ 2 ; = = [ ⃗, ⃗⃗ ] + [ ⃗⃗⃗, ⃗]
⃗
; 2
2
тт
=
+ [ ⃗⃗⃗, ⃗]
∆ ⃗⃗
=
= = тт =
⃗
2
тт
⃗;
; = 2
∆ 0
0
2 ∆
= + ±
⃗ 2 ⃗ ±
⃗ тт =
= ± ;
= ±
⃗
=
=
=
⃗
= ± 2 хурдатгалыг ; ⃗ = = ∆ тт ⃗ хурдсах/ = ⃗⃗ ⃗ ашиглаж тооцоо 2 ⃗ = 0; 2 тт = = ;
удаашрах, муруйх
; =
⃗
= + ⃗ ⃗ 0
0
⃗
0 тт = ∆ ; = = ⃗ = ⃗ ⃗ = ⃗
⃗ ⃗⃗ ⃗⃗ ;
хийдэг, хөдөлгөөн
⃗ = ⃗ + ⃗
⃗⃗ ⃗ = ⃗ + ⃗ тт
0
= ± 2
2 ∆ хөдөлгөөний удаашрах, = ⃗ = ; = ± ⃗= [ ⃗, ⃗⃗ ] + [ ⃗⃗⃗, ⃗]
⃗
2
; =
=
0
⃗ = ⃗ + ⃗
0
тооцоолдог, = ± ± = ; ⃗ = ⃗⃗ ⃗ = ⃗ + ⃗ 2 ; = = = [ ⃗, ⃗⃗ ] + [ ⃗, ]
⃗
⃗
2
=
тооцоо хийдэг.
2
= [ ⃗, ⃗⃗ ] + [ ⃗⃗⃗, ⃗]
=
=
=
⃗
⃗
; = ; =
;
2
= ± 2 ±
0
0 ± = 2
0 = ; =
∆ ⃗⃗ 2 = = 0 = ± ⃗ = жигд, хурдсах/ эсэх гэх мэтээр ∆ = + ⃗ = ⃗ ⃗ ⃗
=
0
⃗⃗
2 =
0
⃗
⃗
+ 2
= ± = 0 ±
⃗
∆ = 2
2
= + ∆
⃗ 2
= ∆ ⃗⃗ ; = тт ± 2 0 ⃗ 2 0 тойргоор эргэх = ⃗ ∆ 2 = = ; = ; = ; =
;
=
⃗
0 ⃗ ⃗
= + ⃗ + ⃗ шинжилгээ хийдэг,
⃗
; =
⃗
⃗⃗ ⃗ = ⃗ + ⃗ =
2
=
хөдөлгөөнийг = ±
∆ = + 2
=
⃗⃗ ;
тт
0
⃗
∆ = ±
⃗
= ∆ ; тт = 0 0 2 ⃗ + ⃗ + 2 тт ⃗⃗ 2 = ⃗ = ⃗ ⃗ = ⃗ 2 ⃗ = ; = 2
хөдөлгөөнийг
=
⃗
∆ = +
⃗; =
⃗ + ⃗ =
⃗= ∆
= = ⃗ удаашрах, ∆
⃗
2
= ⃗ = ; =
⃗; ⃗
⃗ ; ⃗ = 2
⃗ ⃗ ∆
0
⃗⃗
⃗ + ⃗
= ± шинжилдэг. = ∆ ; 0 2 2 = ⃗ = 2 = ∆ + = вектор диаграммаар 2 = =
⃗ ∆ 2
0
⃗
2
⃗ ⃗ ;
; ⃗⃗
⃗; = =
2
2
0
2 =
∆
⃗
⃗
2 2 ⃗ =
муруйх эсэхийг
=
⃗ ∆ ⃗ = ⃗
∆ = + = =
2
⃗ ⃗ ⃗
⃗
⃗;
+
⃗ 2
⃗ = ⃗
= ± 2 ⃗ = ⃗ + 0 ∆ ; + = 0 0 + шинжилдэг. ; = ∆ ∆ 2 ; = = ; 2 = 2 2 ; тт
⃗
2
= ± = ± ⃗
; = =
=
0
∆
; = =
0
2
тт
∆
0 тт = +
2 = =
0 ∆
= ⃗
2
∆ 2
2
= ∆
2 ; =
0
2
=∆ =
0 ±
= 0
= ;
= ± ± = ± = ; тт = 2 2 ± 2 2 2 = шинжилдэг. 2 дүрсэлдэг. 0 0 =
0 =
2
=
=
= 0 +
тт 0 2
∆
∆
;
⃗; = ⃗; ⃗ =
тт = + 2 2
⃗ 2 = +
⃗ ∆
0
=
0
∆ ⃗⃗ ;
⃗
2
2
2
= ⃗ = = ±
⃗ 2
2 0
⃗⃗
⃗
тт
= ±
2
2 + ⃗ =
0
= 2 ± 2 = ∆ ⃗⃗ ⃗ = ⃗ ; 2 2 = 0 ⃗ = = ⃗; = ⃗⃗ = ; тт 2 2 ⃗⃗⃗ ⃗⃗⃗⃗
⃗
2
=
0
⃗
⃗;
± 2 2
⃗ =
⃗
⃗2
⃗
⃗⃗⃗⃗ ⃗ = [ ⃗⃗⃗, ]
2
⃗
⃗
⃗ ⃗ = ⃗ + ⃗ ⃗ =
⃗
⃗
⃗
⃗
∆
= =
= ± 0 2 2 = ∆ ⃗; = ⃗⃗ 2 ± ⃗ = ⃗⃗⃗ ⃗⃗⃗⃗ ⃗ = 2 ⃗⃗ ; ⃗ = 2 = [ ⃗, ⃗⃗ ]
=
⃗
⃗
⃗
⃗⃗⃗; ⃗
= ; =
2
0
= [ ⃗, ⃗⃗ ]
тт ∆ ; ; =
= ± 2 0
=
= = = 2
=
= ;
=
12.1.1с
=
2
= =
= ± 2 ⃗⃗ ∆ = = ⃗ = ∆ = ; = ± ± 2 2 = ; = ; тт = = 2
0
2 ∆
2
=
;
⃗
тт
⃗⃗⃗
⃗
⃗
тт[ ⃗⃗⃗, ⃗⃗ ]
⃗ тт
=
∆ ; ; =
; ⃗ = ⃗⃗⃗⃗
⃗ =
⃗
⃗
2
2
0 0
тт
⃗ ⃗ ; тт =
∆
2
2
0
∆ = + 2 2
= ± 2 ; = 2 ; тт = ; ⃗ ; 2 тт = ∆ = + 2 = ± тт = ; =
⃗
; ⃗
⃗
⃗
⃗ =
⃗ = = =
=
0 ⃗ =
2 2
;
0
= 2
∆
=
∆
2
тт
2 ∆ ⃗⃗
0 0 =
2
;
⃗
= ± 2
2
= ± ±
⃗
0 =
=
⃗
∆ 2
⃗⃗⃗⃗
⃗
⃗
= [ ⃗, ⃗⃗ ] + [ ⃗, ]
∆ ⃗⃗ = ; = ∆ = ⃗ ⃗; ⃗ = ⃗⃗ = ± 0тт = 0 2 0 ⃗⃗⃗ ⃗⃗⃗ ⃗⃗⃗⃗ = [ ⃗, ⃗⃗ ] [ ⃗⃗⃗, ⃗⃗ ]
⃗
⃗
= ±
2
±
=
⃗
⃗
⃗ ⃗; ⃗ =
⃗
⃗
⃗; ;
= ∆ ; тт = ∆ 2 тт = ⃗ = ⃗ ⃗ ⃗ = ⃗⃗ ± тт = тт 2 2 ± 2 2 ⃗⃗⃗ = ⃗⃗⃗⃗ ⃗ ; ⃗ = ⃗⃗⃗; ⃗ = ⃗ ⃗ ⃗ ⃗⃗ ⃗ = ⃗ ⃗ ⃗
⃗
⃗
= [ ⃗, ⃗⃗ ] + [ ⃗⃗⃗, ⃗] ⃗⃗ ]
⃗⃗⃗
⃗ = ⃗⃗⃗ = ⃗⃗⃗⃗
0
= +
⃗
=
0
= [ ⃗, ⃗⃗ ] + [ ⃗, ] ⃗ = [ ⃗⃗⃗, ⃗⃗ ]
⃗⃗ ⃗ = ⃗ + ⃗
= ⃗
⃗ ⃗ = [ ⃗⃗⃗, ⃗⃗ ]
0
⃗ ⃗⃗⃗ =
⃗ = [ ⃗⃗⃗,
0
⃗⃗ ⃗
; = =
⃗ ; ⃗ =
⃗
⃗
⃗
⃗
⃗
⃗
= ± = ∆ ; = тт ± 2 ⃗ ; ⃗ = ; ; ; = ∆ ; = ; = ; = 2 2 ; = = ⃗ = ; ⃗ = ⃗
∆
⃗ = ;
=
= ⃗⃗⃗ =
= ; ⃗ =
2
2
=
= [ ⃗, ⃗⃗ ] + [ ⃗⃗⃗, ⃗]
⃗
∆
тт
⃗ = ⃗ =
⃗
⃗
0
;
= ⃗ = 2
= ∆
=
⃗
= ;
⃗ ⃗⃗
= = ⃗ =
⃗ = ⃗ + ⃗ =
= ± ∆ = ± = 0 = 2 ⃗ = ⃗ + ⃗ ∆ ; = = 0 ± 0 ; ; = ⃗ ⃗
0
тт
тт
⃗ = ⃗ + ⃗ +
= ± ± =
⃗
= ±
0 ⃗⃗⃗⃗ =
2 ⃗⃗
0 = =
∆
∆
∆
⃗
±
0
0
⃗ = ⃗ + ⃗ =
; ; =
⃗ =
⃗⃗⃗ = ;
0 ⃗
=
= ± =
0
⃗⃗
= ±
= [ ⃗, ⃗⃗ ] + [ ⃗, ] + [ ⃗⃗⃗, ⃗]
2
⃗ =
⃗ ⃗⃗ ⃗ = = ⃗ + ⃗
⃗⃗
⃗
⃗
⃗
⃗ ⃗⃗ ]
=
= [ ⃗,
∆ 0
=
⃗
∆
⃗⃗ ± 2
⃗
2
2
0
⃗
0
= 0 ⃗ • Материал ⃗ + ⃗ + 2 2= ⃗ + ⃗ = ⃗ ⃗⃗⃗ ; ⃗ = ⃗⃗⃗⃗ ⃗ = [ ⃗⃗⃗, ⃗⃗ ] = ⃗ ⃗ = ⃗⃗ ] + [ ⃗⃗⃗, ⃗] ⃗ ⃗ ⃗ ⃗
0
= 2 ⃗ =
⃗
⃗
= [ ⃗, ⃗⃗ ] + [ ⃗, ]
= [ ⃗, ⃗⃗ ] ⃗ =
= [ ⃗,
⃗ ⃗⃗ ⃗⃗
⃗ ⃗ = 2
2
⃗
⃗
2
⃗
⃗ ; = ±
= + ⃗ + ⃗
; ⃗ =
⃗⃗⃗ =
⃗
∆ ⃗
= [ ⃗, ⃗⃗ ] + [ ⃗, ] ⃗ = [ ⃗⃗⃗, ⃗] = [ ⃗⃗⃗, [ ⃗⃗⃗, ⃗⃗ ]]
⃗
= ⃗ =
⃗ 2
; =
0
= ± = ± ; 2 цэгийн эргэх ⃗⃗ ; = 2 ⃗ ⃗ ⃗ = ⃗ = + ∆ ∆ = + ⃗ = 2 ⃗ ⃗ ⃗
⃗
⃗ ∆
⃗
2 2 ⃗ =
=
0 ±
= + ⃗
= 2
⃗
∆
; =
2
0
= ± ; =
2
2
= = ±
2
∆ ⃗⃗
2
0
⃗
⃗ = ⃗ +
=
= ±
∆ = +
= ± =
0 ;
0
0
⃗ =
=
хөдөлгөөний ⃗ + ⃗ +
0
=
⃗ =
±
⃗
0
2
0
⃗
0
= ± ∆ = ± ∆ = +
2 ⃗ = ⃗ + + = 2 0 ; = ∆ ⃗; = 2 0 ⃗ 2 ∆ ⃗ 0 2 = [ ⃗, ⃗⃗ ]; = ⃗( ⃗, ⃗⃗ )
⃗
⃗
⃗
= [ ⃗, ⃗⃗ ] + [ ⃗⃗⃗, ⃗]
⃗
2
⃗
0
0
0 2
0
2
2
⃗ 2
=
⃗; =
⃗
2
2
∆
2
2 ∆ ⃗⃗ 2 2 ⃗⃗ өнцөг хурд, томьёонуудыг ⃗⃗ ⃗ ⃗ = ⃗ = [ ⃗, ⃗⃗ ] + [ ⃗, ] =
⃗
⃗⃗ ⃗ = ⃗ + ⃗ =
⃗
⃗
⃗
= ; = 2 = ∆ ; тт = ⃗; = 2 = = = ; тт ⃗ = ⃗ − ⃗⃗
2
⃗
2
2
⃗
⃗
=
= =
=
өнцөг ⃗ ⃗
тт
2
⃗
2
⃗ ∆ 2
2
;
= ± = ∆ ⃗⃗ ± = = + 2 тт = ашиглаж эргэх тт = 2 ± = ; тт 2 ⃗ = [ ⃗⃗⃗, ⃗] = [ ⃗⃗⃗, [ ⃗⃗⃗, ⃗⃗ ]] = ⃗⃗⃗( ⃗⃗⃗, ⃗⃗ ) − ⃗⃗
∆ 0
∆
= =
2
∆
=
=
тт
⃗
;
тт 2
0
⃗ ; ; =
0
=
2 ∆ = ∆ ; тт ; = ⃗ = = ; = ± 0 2 = = ; тт ⃗⃗⃗ ⃗⃗⃗⃗
0 = ±
=
томьёонуудыг 2
= [ ⃗, ⃗⃗ ]
хурдатгалыг
= ± ⃗ ⃗ = хөдөлгөөний 2 2 ; = ⃗⃗⃗ ⃗] = [ ⃗⃗⃗, [ ⃗⃗⃗, ⃗⃗ ]] = ⃗⃗⃗( ⃗⃗⃗, ⃗⃗ ) − ⃗⃗
2
томьёонуудыг
⃗
⃗
⃗
⃗ =
⃗
; ⃗ =
⃗
2
= ±
; =
⃗
=
⃗
⃗
шугаман хурд, = ±
⃗
2 0 ∆ ⃗⃗ 2 = ⃗ ; 0 ашиглаж эргэх = [ ⃗, ⃗⃗⃗⃗ ⃗
⃗
⃗
∆ ⃗⃗ = ; = өнцөг 2 ; = ⃗⃗⃗ ⃗ = ⃗⃗⃗⃗ ; ⃗ = = [ ⃗, ⃗⃗ ] 1 2
⃗
⃗
2
⃗
0
ашиглаж эргэх
;
=
2
⃗
хөдөлгөөний
⃗⃗ ⃗
= 2
= ; тт = = ± тт ⃗ ⃗ ⃗ = хурдатгалтай ⃗ = ⃗ + ⃗ = ± тт = ⃗ = ; = ⃗ = [ ⃗⃗⃗, ⃗⃗
⃗
] =
; ⃗ =
⃗
0
∆
⃗
тт
2
=
∆ ⃗ = 2 = ; ; = ⃗⃗ ; шилжилт, хурд, хөдөлгөөний томьёонуудыг
⃗
0
= + = ±
⃗
⃗
холбодог,
2
⃗
⃗
⃗
⃗
=
2
ашиглаж эргэх
0 ±
; =
өнцөг
⃗ =
= ± = ± = ⃗⃗ = + = 0 ± 0 ; = 0 ; = ⃗ = [ ⃗, ⃗⃗ ] + [ ⃗⃗⃗, ⃗]
⃗
2
=
хурдатгалын
∆ = +
=
шилжилт, хурд, өнцөг шилжилт,
⃗
⃗
⃗
=
⃗
тайлбарладаг.
= [ ⃗, ⃗⃗ ] + [ ⃗, ] =
2
0
; =
2
хөдөлгөөний
⃗
= [ ⃗, ⃗⃗ ] + [ ⃗⃗⃗, ⃗]
2 ⃗⃗
0 = ± ⃗⃗ = ⃗⃗ = = ⃗⃗ тооцоо хийдэг. ∆ = + ⃗ = 2 ⃗ = ⃗ ⃗
0
⃗
⃗ = ⃗ + ⃗
⃗
⃗
2
0
⃗⃗
=
⃗
= = 2 ⃗ = ⃗ + ⃗ ⃗ ⃗ + ⃗ ⃗; = хурдатгалын хурд, хурдатгалын
⃗
⃗
2
2
⃗
⃗
⃗ ⃗
⃗
⃗
2
2 = ∆ ; 2 = + = ⃗; = ⃗ 2 = ; = = параметрийн
тооцоо хийдэг. тооцоо хийдэг.
2
=
тооцоо хийдэг,
=
тт
тт
= ± = ∆ ± = 2 ∆ = + = = = ,
∆ 0
2
;
0
2
⃗
2 ∆ тт 2 2 ∆ = + 2 = ; 0 тт 2 2
0
2
⃗
0 =
=
⃗
= ⃗; = = ± ⃗; ⃗ ⃗ ⃗⃗⃗ ⃗⃗⃗⃗ вектор диаграммаар
⃗
⃗
⃗
⃗ 2 = ± 2 ⃗ = ; ⃗ = = [ ⃗, ⃗⃗ ]
⃗
⃗
⃗
⃗
⃗
дүрсэлдэг.
⃗ =
2 ∆ ⃗⃗⃗ ⃗⃗⃗⃗
2
∆ = = = 0 2 2 = = [ ⃗, ⃗⃗ ] = −
⃗
⃗
⃗ = = ;
⃗ ; ;
; ⃗
= ; тт = ∆ тт = ; тт = = = тт ⃗ ⃗
;
⃗
2
∆ ⃗ = 2 = ±
0
= ± ⃗
= ±
⃗⃗⃗
⃗⃗⃗⃗
⃗⃗ ⃗ = ± 0 0 2 ⃗⃗⃗ ⃗⃗⃗⃗ = ⃗⃗⃗ = [ ⃗, ⃗⃗ ] + [ ⃗⃗⃗, ⃗] [ ⃗⃗⃗, ⃗⃗ ]
⃗ =
⃗
⃗
; ⃗ =
0
;
⃗ = = + 2 ⃗ = ; ⃗ = = [ ⃗, ⃗⃗ ] =
⃗
⃗
⃗
⃗
⃗
⃗
⃗
⃗
⃗
⃗
=
⃗
⃗
= +
⃗
⃗
= ; = ⃗⃗ ⃗ ⃗ ⃗ ⃗ = = [ ⃗, ⃗⃗ ] + [ ⃗, ]
⃗
= ± = ± ⃗
0
⃗
⃗
⃗⃗ 0 ⃗ = = [ ⃗, ⃗⃗ ] + [ ⃗, ]
⃗
⃗
⃗
⃗
⃗
⃗
⃗⃗ = = + = = [ ⃗, ⃗⃗ ] + [ ⃗, ]
⃗
⃗
⃗
⃗
⃗
⃗
⃗
= = +
⃗
125